Axiom Math Definition
Axiom Math Definition - Axioms or postulate is defined as a statement that is accepted as true and correct, called as a theorem in mathematics. An axiom is a statement that is true or assumed to be true without any proof whereas a theorem must be proven. An axiom serves as the base. It is accepted as true, without proof, as the basis for argument.
It is accepted as true, without proof, as the basis for argument. An axiom is a statement that is true or assumed to be true without any proof whereas a theorem must be proven. An axiom serves as the base. Axioms or postulate is defined as a statement that is accepted as true and correct, called as a theorem in mathematics.
An axiom serves as the base. An axiom is a statement that is true or assumed to be true without any proof whereas a theorem must be proven. It is accepted as true, without proof, as the basis for argument. Axioms or postulate is defined as a statement that is accepted as true and correct, called as a theorem in mathematics.
What Are Axioms? YouTube
An axiom is a statement that is true or assumed to be true without any proof whereas a theorem must be proven. It is accepted as true, without proof, as the basis for argument. Axioms or postulate is defined as a statement that is accepted as true and correct, called as a theorem in mathematics. An axiom serves as the.
Definition of Axiom YouTube
It is accepted as true, without proof, as the basis for argument. An axiom is a statement that is true or assumed to be true without any proof whereas a theorem must be proven. An axiom serves as the base. Axioms or postulate is defined as a statement that is accepted as true and correct, called as a theorem in.
Discrete Mathematics Chapter 1 Logic and proofs 1282020
An axiom is a statement that is true or assumed to be true without any proof whereas a theorem must be proven. Axioms or postulate is defined as a statement that is accepted as true and correct, called as a theorem in mathematics. An axiom serves as the base. It is accepted as true, without proof, as the basis for.
PPT Axiomatic Systems PowerPoint Presentation, free download ID4520354
An axiom is a statement that is true or assumed to be true without any proof whereas a theorem must be proven. It is accepted as true, without proof, as the basis for argument. Axioms or postulate is defined as a statement that is accepted as true and correct, called as a theorem in mathematics. An axiom serves as the.
What is an axiom?
Axioms or postulate is defined as a statement that is accepted as true and correct, called as a theorem in mathematics. It is accepted as true, without proof, as the basis for argument. An axiom serves as the base. An axiom is a statement that is true or assumed to be true without any proof whereas a theorem must be.
Solved What axiom can justify this statement 9* (8+5)=(9* 8)+(9* 5
It is accepted as true, without proof, as the basis for argument. An axiom is a statement that is true or assumed to be true without any proof whereas a theorem must be proven. Axioms or postulate is defined as a statement that is accepted as true and correct, called as a theorem in mathematics. An axiom serves as the.
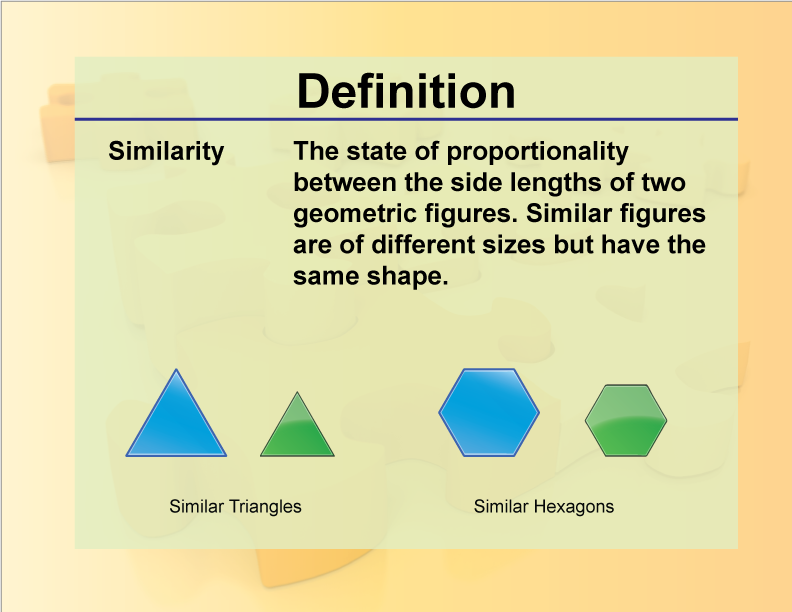
DefinitionGeometry BasicsSimilarity Media4Math
Axioms or postulate is defined as a statement that is accepted as true and correct, called as a theorem in mathematics. It is accepted as true, without proof, as the basis for argument. An axiom serves as the base. An axiom is a statement that is true or assumed to be true without any proof whereas a theorem must be.
What is an axiom?
An axiom is a statement that is true or assumed to be true without any proof whereas a theorem must be proven. Axioms or postulate is defined as a statement that is accepted as true and correct, called as a theorem in mathematics. An axiom serves as the base. It is accepted as true, without proof, as the basis for.
Physics; formulated so as to be indubitable and thus forming a final
Axioms or postulate is defined as a statement that is accepted as true and correct, called as a theorem in mathematics. An axiom serves as the base. An axiom is a statement that is true or assumed to be true without any proof whereas a theorem must be proven. It is accepted as true, without proof, as the basis for.
What is an Axiom Definition of Axiom
It is accepted as true, without proof, as the basis for argument. An axiom serves as the base. An axiom is a statement that is true or assumed to be true without any proof whereas a theorem must be proven. Axioms or postulate is defined as a statement that is accepted as true and correct, called as a theorem in.
It Is Accepted As True, Without Proof, As The Basis For Argument.
Axioms or postulate is defined as a statement that is accepted as true and correct, called as a theorem in mathematics. An axiom is a statement that is true or assumed to be true without any proof whereas a theorem must be proven. An axiom serves as the base.