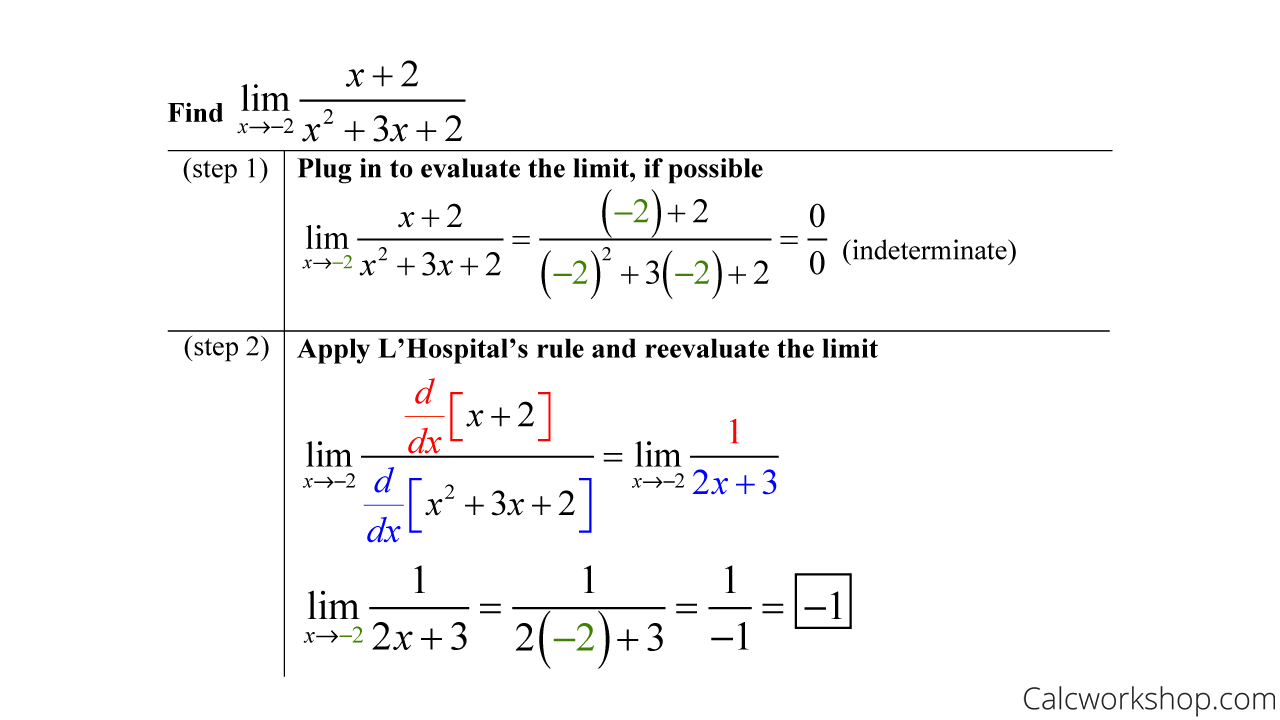Indeterminate Form And L Hospital Rule
Indeterminate Form And L Hospital Rule - In evaluating limits, we must recognize when direct substitution leads to an indeterminate form. Example 1 evaluate each limit. Although they are not numbers, these indeterminate forms play a useful role in the limiting behaviour of a function. Before applying l’hospital’s rule, check to see that the limit has one of the indeterminate forms. In order to use l’h^opital’s rule, we need to check. L’hospital’s rule works great on the two indeterminate forms 0/0 and \({{ \pm \,\infty }}/{{ \pm \,\infty }}\;\). Let us return to limits (chapter 1) and see how we can use derivatives to simplify certain families of limits called indeterminate. The following forms are indeterminate. Know how to compute derivatives, we can use l’h^opital’s rule to check that this is correct.
Let us return to limits (chapter 1) and see how we can use derivatives to simplify certain families of limits called indeterminate. Example 1 evaluate each limit. L’hospital’s rule works great on the two indeterminate forms 0/0 and \({{ \pm \,\infty }}/{{ \pm \,\infty }}\;\). The following forms are indeterminate. Know how to compute derivatives, we can use l’h^opital’s rule to check that this is correct. In order to use l’h^opital’s rule, we need to check. Although they are not numbers, these indeterminate forms play a useful role in the limiting behaviour of a function. Before applying l’hospital’s rule, check to see that the limit has one of the indeterminate forms. In evaluating limits, we must recognize when direct substitution leads to an indeterminate form.
L’hospital’s rule works great on the two indeterminate forms 0/0 and \({{ \pm \,\infty }}/{{ \pm \,\infty }}\;\). Know how to compute derivatives, we can use l’h^opital’s rule to check that this is correct. In evaluating limits, we must recognize when direct substitution leads to an indeterminate form. Let us return to limits (chapter 1) and see how we can use derivatives to simplify certain families of limits called indeterminate. Example 1 evaluate each limit. Although they are not numbers, these indeterminate forms play a useful role in the limiting behaviour of a function. Before applying l’hospital’s rule, check to see that the limit has one of the indeterminate forms. In order to use l’h^opital’s rule, we need to check. The following forms are indeterminate.
A Gentle Introduction to Indeterminate Forms and L’Hospital’s Rule
The following forms are indeterminate. Before applying l’hospital’s rule, check to see that the limit has one of the indeterminate forms. Let us return to limits (chapter 1) and see how we can use derivatives to simplify certain families of limits called indeterminate. Know how to compute derivatives, we can use l’h^opital’s rule to check that this is correct. In.
A Gentle Introduction to Indeterminate Forms and L’Hospital’s Rule
Know how to compute derivatives, we can use l’h^opital’s rule to check that this is correct. In order to use l’h^opital’s rule, we need to check. L’hospital’s rule works great on the two indeterminate forms 0/0 and \({{ \pm \,\infty }}/{{ \pm \,\infty }}\;\). Although they are not numbers, these indeterminate forms play a useful role in the limiting behaviour.
A Gentle Introduction to Indeterminate Forms and L’Hospital’s Rule
L’hospital’s rule works great on the two indeterminate forms 0/0 and \({{ \pm \,\infty }}/{{ \pm \,\infty }}\;\). The following forms are indeterminate. Although they are not numbers, these indeterminate forms play a useful role in the limiting behaviour of a function. In evaluating limits, we must recognize when direct substitution leads to an indeterminate form. In order to use.
L'hopital's Rule Calculator With Steps Free
Know how to compute derivatives, we can use l’h^opital’s rule to check that this is correct. In order to use l’h^opital’s rule, we need to check. Although they are not numbers, these indeterminate forms play a useful role in the limiting behaviour of a function. The following forms are indeterminate. Let us return to limits (chapter 1) and see how.
Indeterminate Forms & L’Hospital’s Rule Practice "Get the Same Answer
Although they are not numbers, these indeterminate forms play a useful role in the limiting behaviour of a function. Before applying l’hospital’s rule, check to see that the limit has one of the indeterminate forms. The following forms are indeterminate. In evaluating limits, we must recognize when direct substitution leads to an indeterminate form. In order to use l’h^opital’s rule,.
L Hopital's Rule Calculator
In evaluating limits, we must recognize when direct substitution leads to an indeterminate form. Although they are not numbers, these indeterminate forms play a useful role in the limiting behaviour of a function. Before applying l’hospital’s rule, check to see that the limit has one of the indeterminate forms. Know how to compute derivatives, we can use l’h^opital’s rule to.
4.5a Indeterminate Forms and L'Hopital's Rule YouTube
In evaluating limits, we must recognize when direct substitution leads to an indeterminate form. L’hospital’s rule works great on the two indeterminate forms 0/0 and \({{ \pm \,\infty }}/{{ \pm \,\infty }}\;\). Example 1 evaluate each limit. Before applying l’hospital’s rule, check to see that the limit has one of the indeterminate forms. Although they are not numbers, these indeterminate.
MakeTheBrainHappy LHospital's Rule for Indeterminate Forms
In order to use l’h^opital’s rule, we need to check. Although they are not numbers, these indeterminate forms play a useful role in the limiting behaviour of a function. Before applying l’hospital’s rule, check to see that the limit has one of the indeterminate forms. L’hospital’s rule works great on the two indeterminate forms 0/0 and \({{ \pm \,\infty }}/{{.
Indeterminate Forms and L' Hospital Rule
Example 1 evaluate each limit. L’hospital’s rule works great on the two indeterminate forms 0/0 and \({{ \pm \,\infty }}/{{ \pm \,\infty }}\;\). In order to use l’h^opital’s rule, we need to check. Although they are not numbers, these indeterminate forms play a useful role in the limiting behaviour of a function. Before applying l’hospital’s rule, check to see that.
Indeterminate Form & L'Hospital's Rule Limits of the Indeterminate
L’hospital’s rule works great on the two indeterminate forms 0/0 and \({{ \pm \,\infty }}/{{ \pm \,\infty }}\;\). Example 1 evaluate each limit. The following forms are indeterminate. Before applying l’hospital’s rule, check to see that the limit has one of the indeterminate forms. In evaluating limits, we must recognize when direct substitution leads to an indeterminate form.
The Following Forms Are Indeterminate.
L’hospital’s rule works great on the two indeterminate forms 0/0 and \({{ \pm \,\infty }}/{{ \pm \,\infty }}\;\). In evaluating limits, we must recognize when direct substitution leads to an indeterminate form. Before applying l’hospital’s rule, check to see that the limit has one of the indeterminate forms. Let us return to limits (chapter 1) and see how we can use derivatives to simplify certain families of limits called indeterminate.
In Order To Use L’h^opital’s Rule, We Need To Check.
Example 1 evaluate each limit. Although they are not numbers, these indeterminate forms play a useful role in the limiting behaviour of a function. Know how to compute derivatives, we can use l’h^opital’s rule to check that this is correct.