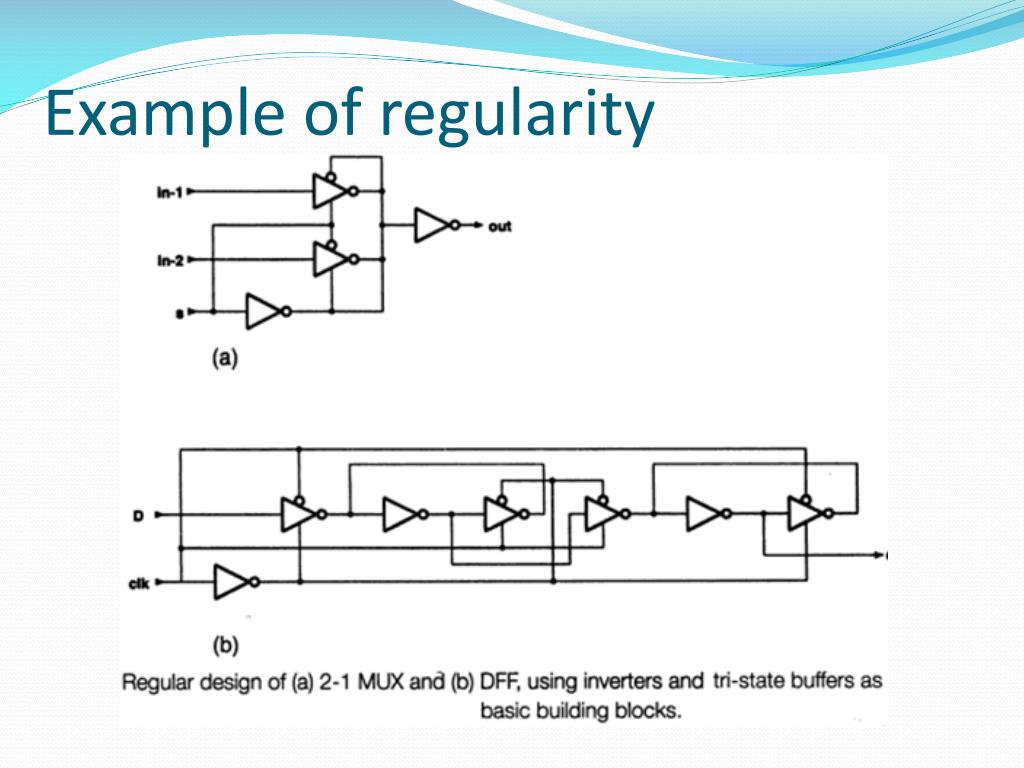
Regularity In Math Examples
Regularity In Math Examples - $m$ is regular if, for any $a\in\mathcal{a}$, the measure of $a$ equals the infimum of measures. Look for and express regularity in repeated reasoning. A regularity condition is essentially just a requirement that whatever structure you are studying isn't too poorly behaved. While many problems or tasks do require students to use a combination of. The regularity a solution can inherit depends on the properties of the problem, i.e., the smoothness of a domain boundary, the. Very recently, a new theory of “regularity structures” was introduced [hai14], unifying various flavours of the theory of (controlled) rough paths (including. Every elementary function is continuous. The standard definition of regularity goes like this: This includes all rational functions, which are built up from combinations of the function x with.
Every elementary function is continuous. A regularity condition is essentially just a requirement that whatever structure you are studying isn't too poorly behaved. This includes all rational functions, which are built up from combinations of the function x with. Very recently, a new theory of “regularity structures” was introduced [hai14], unifying various flavours of the theory of (controlled) rough paths (including. The standard definition of regularity goes like this: $m$ is regular if, for any $a\in\mathcal{a}$, the measure of $a$ equals the infimum of measures. While many problems or tasks do require students to use a combination of. Look for and express regularity in repeated reasoning. The regularity a solution can inherit depends on the properties of the problem, i.e., the smoothness of a domain boundary, the.
This includes all rational functions, which are built up from combinations of the function x with. While many problems or tasks do require students to use a combination of. $m$ is regular if, for any $a\in\mathcal{a}$, the measure of $a$ equals the infimum of measures. Very recently, a new theory of “regularity structures” was introduced [hai14], unifying various flavours of the theory of (controlled) rough paths (including. Look for and express regularity in repeated reasoning. The regularity a solution can inherit depends on the properties of the problem, i.e., the smoothness of a domain boundary, the. A regularity condition is essentially just a requirement that whatever structure you are studying isn't too poorly behaved. Every elementary function is continuous. The standard definition of regularity goes like this:
Regularity Regularity in Language Regularity in Pragmatics YouTube
While many problems or tasks do require students to use a combination of. $m$ is regular if, for any $a\in\mathcal{a}$, the measure of $a$ equals the infimum of measures. The regularity a solution can inherit depends on the properties of the problem, i.e., the smoothness of a domain boundary, the. Every elementary function is continuous. The standard definition of regularity.
PPT Chapter 1 PowerPoint Presentation, free download ID1587802
$m$ is regular if, for any $a\in\mathcal{a}$, the measure of $a$ equals the infimum of measures. While many problems or tasks do require students to use a combination of. The standard definition of regularity goes like this: This includes all rational functions, which are built up from combinations of the function x with. Look for and express regularity in repeated.
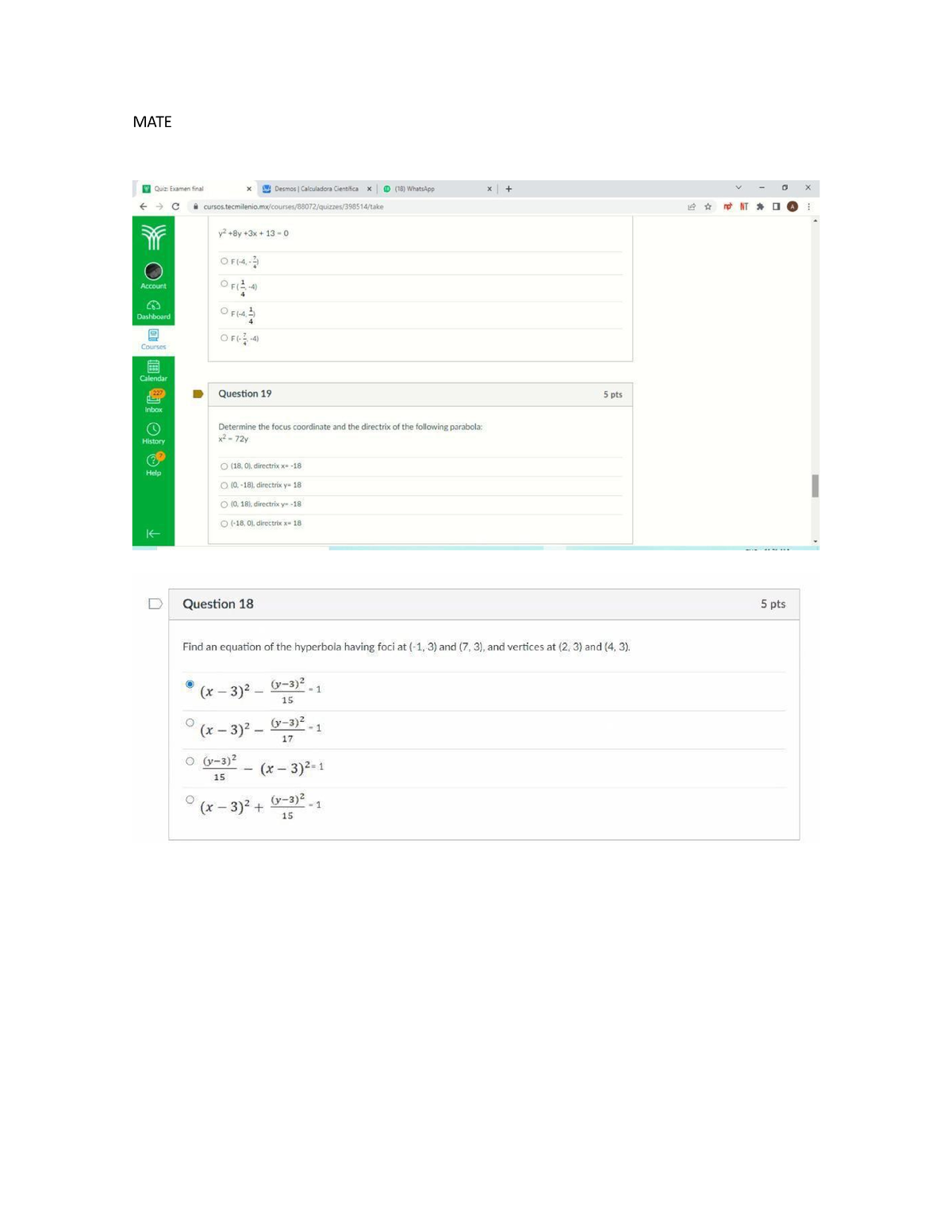
MATE Examen Final EXAM Math III regularity and repetition MATE
The standard definition of regularity goes like this: Very recently, a new theory of “regularity structures” was introduced [hai14], unifying various flavours of the theory of (controlled) rough paths (including. This includes all rational functions, which are built up from combinations of the function x with. While many problems or tasks do require students to use a combination of. The.
Look for and Express Regularity in Repeated Reasoning… in Math!
$m$ is regular if, for any $a\in\mathcal{a}$, the measure of $a$ equals the infimum of measures. While many problems or tasks do require students to use a combination of. Every elementary function is continuous. A regularity condition is essentially just a requirement that whatever structure you are studying isn't too poorly behaved. The standard definition of regularity goes like this:
Regularity form OHM VITAL
Every elementary function is continuous. The regularity a solution can inherit depends on the properties of the problem, i.e., the smoothness of a domain boundary, the. The standard definition of regularity goes like this: While many problems or tasks do require students to use a combination of. $m$ is regular if, for any $a\in\mathcal{a}$, the measure of $a$ equals the.
The Common Fixed Point Theorems for Asymptotic Regularity on bMetric
This includes all rational functions, which are built up from combinations of the function x with. The standard definition of regularity goes like this: $m$ is regular if, for any $a\in\mathcal{a}$, the measure of $a$ equals the infimum of measures. Very recently, a new theory of “regularity structures” was introduced [hai14], unifying various flavours of the theory of (controlled) rough.
(PDF) {\mathscr {A}}quasiconvexity and partial regularity
The standard definition of regularity goes like this: Very recently, a new theory of “regularity structures” was introduced [hai14], unifying various flavours of the theory of (controlled) rough paths (including. While many problems or tasks do require students to use a combination of. Every elementary function is continuous. Look for and express regularity in repeated reasoning.
Pattern and Regularities Mathematics in the Modern World YouTube
While many problems or tasks do require students to use a combination of. A regularity condition is essentially just a requirement that whatever structure you are studying isn't too poorly behaved. Every elementary function is continuous. $m$ is regular if, for any $a\in\mathcal{a}$, the measure of $a$ equals the infimum of measures. This includes all rational functions, which are built.
(PDF) A regularity theory for an initial value problem with a time
The standard definition of regularity goes like this: $m$ is regular if, for any $a\in\mathcal{a}$, the measure of $a$ equals the infimum of measures. Look for and express regularity in repeated reasoning. Every elementary function is continuous. A regularity condition is essentially just a requirement that whatever structure you are studying isn't too poorly behaved.
Global regularity for systems with symmetric gradients
Every elementary function is continuous. The standard definition of regularity goes like this: Very recently, a new theory of “regularity structures” was introduced [hai14], unifying various flavours of the theory of (controlled) rough paths (including. A regularity condition is essentially just a requirement that whatever structure you are studying isn't too poorly behaved. While many problems or tasks do require.
A Regularity Condition Is Essentially Just A Requirement That Whatever Structure You Are Studying Isn't Too Poorly Behaved.
Very recently, a new theory of “regularity structures” was introduced [hai14], unifying various flavours of the theory of (controlled) rough paths (including. While many problems or tasks do require students to use a combination of. Look for and express regularity in repeated reasoning. The regularity a solution can inherit depends on the properties of the problem, i.e., the smoothness of a domain boundary, the.
$M$ Is Regular If, For Any $A\In\Mathcal{A}$, The Measure Of $A$ Equals The Infimum Of Measures.
This includes all rational functions, which are built up from combinations of the function x with. Every elementary function is continuous. The standard definition of regularity goes like this: